User Tools
Sidebar
This is an old revision of the document!
Computational haemodynamics
Model of Blood Circulation
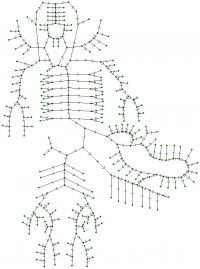
The model is based on the set of differential equations: mass and momentum balance laws, state equation. The vessels are connected with each other at the nodes and with the heart inlets/outlets through the boundary conditions set that is formed by Poiseuille's pressure drop conditions, mass balance equation combined with the appropriate compatibility condition. The model allows us to calculate cross section of every vessel, pressure and velocity of blood everywhere in the cardiovascular system in any moment of time. We can take into consideration hemorrhages, effects of different forces, the spread of drugs. To study influence of implants or pathologies on the blood flow we use more mathematical models.
Fiber model of the elastic vessel wall
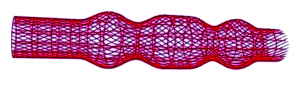
The wall is represented by the set of fibers. We imitate the response of the elastic surface to a deformation as the response of fiber collection to the same deformation.

By such representation we can simulate elastic properties of healthy vessels and vessels with implants (for example cava-filter).
Simulation model of atherosclerotic plaque
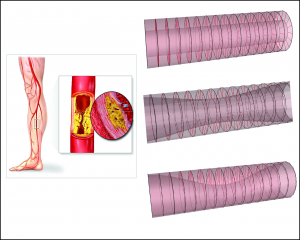
Three-layer structure in the model corresponds to anatomy of real plaque. The wall and fibrous cap are represented by the set of fibers, lipid pool is represented by the set of springs. The model allows us to reproduce elastic properties of atherosclerotic vessel wall.
3D modelling of blood flow
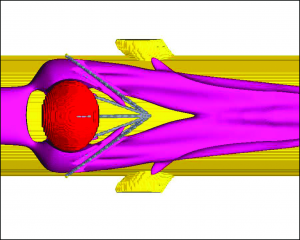
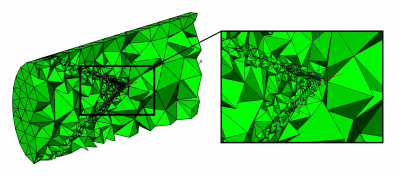
This method is based on the system of Navier-Stokes equations and allows us to describe blood flow in details in the domain of interest (for example near the cava-filter with thrombus).
The example of the adaptive mesh for the flow over a model cava filter problem.
Modelling of blood flow in networks of vessels with pathologies


Atherosclerosis and placed implants such as cava-filters and stents can be taken into consideration by the model of blood circulation in two ways:
1)through the state equation. This pressure dependence of cross section can be modified by means of fiber model of the elastic vessel wall or by the model of atherosclerotic plaque.
2)we describe blood flow in 3D domain of interest and couple it with the 1D model of global blood circulation.
Friendly graphical interface for models
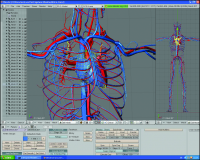
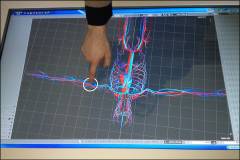
Touchpad for work with models and for visualization of results.
search?q=playground%3Ablood-flow.mp4%20240%2C320%20autoBuffering&btnI=lucky
search?q=playground%3Ablood-pressure.mp4%20360%2C240%20autoBuffering&btnI=lucky search?q=playground%3Ablood-velocity.mp4%20360%2C240%20autoBuffering&btnI=lucky
Team members:
Vassilevski Yuri (INM RAS), Simakov Sergey (MIPT), Maxim Olshanskii (University of Houston), Salamatova Victoria (SEC INM RAS), Ivanov Yuri (INM RAS), Dobroserdova Tatiana (MSU), Kramarenko Vasiliy (MIPT), Gamilov Timur (MIPT)
Working group on mathematical models and numerical methods in biomathematics
http://dodo.inm.ras.ru/biomath/
Ph.D. thesis
Publications on haemodynamics: