Research

Computational haemodynamics

Model of Blood Circulation

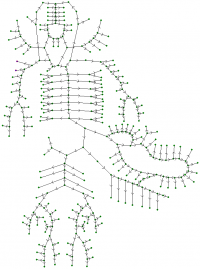
The model is based on the set of differential equations: mass and momentum balance laws, state equation. The vessels are connected with each other at the nodes and with the heart inlets/outlets through the boundary conditions set that is formed by Poiseuille's pressure drop conditions, mass balance equation combined with the appropriate compatibility condition. The model allows us to calculate cross section of every vessel, pressure and velocity of blood everywhere in the cardiovascular system in any moment of time. We can take into consideration hemorrhages, effects of different forces, the spread of drugs. To study influence of implants or pathologies on the blood flow we use more mathematical models.

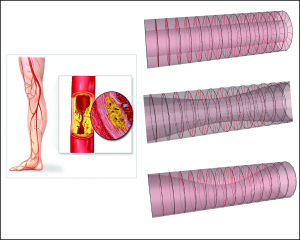
Fiber model of the elastic vessel wall

The wall is represented by the set of fibers. We imitate the response of the elastic surface to a deformation as the response of fiber collection to the same deformation.

By such representation we can simulate elastic properties of healthy vessels and vessels with implants (for example cava-filter).

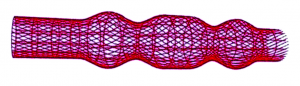
Simulation model of atherosclerotic plaque

Three-layer structure in the model corresponds to anatomy of real plaque. The wall and fibrous cap are represented by the set of fibers, lipid pool is represented by the set of springs. The model allows us to reproduce elastic properties of atherosclerotic vessel wall.

3D modelling of blood flow

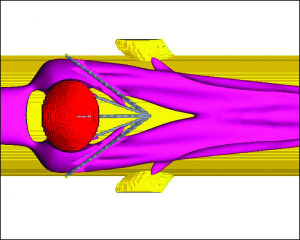
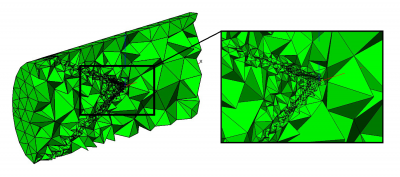
This method is based on the system of Navier-Stokes equations and allows us to describe blood flow in details in the domain of interest (for example near the cava-filter with thrombus).

The example of the adaptive mesh for the flow over a model cava filter problem.

Modelling of blood flow in networks of vessels with pathologies

Atherosclerosis and placed implants such as cava-filters and stents can be taken into consideration by the model of blood circulation in two ways:
1)through the state equation. This pressure dependence of cross section can be modified by means of fiber model of the elastic vessel wall or by the model of atherosclerotic plaque.
2)we describe blood flow in 3D domain of interest and couple it with the 1D model of global blood circulation.

Friendly graphical interface for models

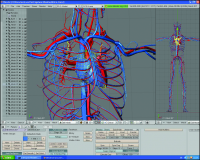
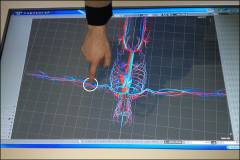
Touchpad for work with models and for visualization of results.

Team members:

Vassilevski Yuri (INM RAS), Simakov Sergey (MIPT), Maxim Olshanskii (University of Houston), Salamatova Victoria (SEC INM RAS), Dobroserdova Tatiana (MSU), Kramarenko Vasiliy (MIPT), Gamilov Timur (MIPT), Pryamonosov Roman (INM RAS)

Working group on mathematical models and numerical methods in biomathematics

http://dodo.inm.ras.ru/biomath/

Ph.D. thesis

Dobroserdova T. Mathematical Modelling of Blood Flow in the vessel network with pathologies or implants. (in Russian)

Publications on haemodynamics:

T.Dobroserdova, M.Olshanskii, S.Simakov. Multiscale coupling of compliant and rigid walls blood flow models. Int. J. Numer. Meth. Fluids, Volume 82, Issue 12, 2016, pages 799–817 doi: 10.1002/fld.4241 (2016).

Computational simulations of fractional flow reserve variability. T.Gamilov, Ph.Kopylov, S.Simakov. In: Numerical Mathematics and Advanced Applications - ENUMATH 2015 (Bülent Karasözen, Murat Manguoglu, Münevver Tezer-Sezgin, Serdar Göktepe, Ömür Ugur eds.). Lecture Notes in Computational Science and Engineering, Springer, 2016

Yu.Vassilevski, T.Gamilov, Ph.Kopylov Personalized computation of fractional flow reserve in case of two consecuteve stenoses. In: Proceedings of VII European Congress on Computational Methods in Applied Sciences and Engineering (M. Papadrakakis, V. Papadopoulos, G. Stefanou, V. Plevris eds.) 2016

S.S.Simakov, T.M.Gamilov, Ph.Yu.Kopylov, Yu.V.Vassilevski Computational study of multivessel coronary disease: haemodynamic significance of stenoses in simulation. Bulletin of experimental biology and medicine, 162(7), 128-131, 2016

N.Bessonov, A.Sequeira, S.Simakov, Yu.Vassilevski, V.Volpert, Methods of Blood Flow Modelling. Mathematical Modelling of Natural Phenomena, 11(1), 1-25, 2016

Ph.Kopylov, A.Bykova, Yu.Vassilevski, S.Simakov. Role of measurement of fractional flow reserve (FFR) in coronary artery atherosclerosis, Therapeutic archive, 87(9), 106-113, 2015

T.M. Gamilov, P.Yu. Kopylov, R.A. Pryamonosov, S.S. Simakov. Virtual fractional flow reserve assessment in patient-specic coronary networks by 1D hemodynamic model. Russian Journal of Numerical Analysis and Mathematical Modelling. 30(5), 269–276 (2015)