Инструменты пользователя
Боковая панель
Содержание
Kirill Dm. Nikitin
Contacts
- e-mail: nikitin.kira (at) gmail.com
- LinkedIn: Kirill Nikitin
Member of
Publications
Free surface flows
[1] K. Nikitin, Y.Vassilevski, R.Yanbarisov, «An implicit scheme for simulation of free surface non-Newtonian fluid flows on dynamically adapted grids» // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol. 36, I. 3, (June 2021), pp. 165-176. PDF
[2] K. Nikitin, K.Terekhov, Y.Vassilevski, «Two methods of surface tension treatment in free surface flow simulations» // Applied Mathematics Letters, Vol. 86, (December 2018), pp. 236-242. PDF
[3] K. Nikitin, M.Olshanskii, K.Terekhov, Y.Vassilevski, «A splitting method for free surface flows over partially submerged obstacles» // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol. 33, No. 2, (2018), pp. 95-110. PDF
[4] K. Nikitin, M. Olshanskii, K. Terekhov, Y. Vassilevski, R. Yanbarisov. «An adaptive numerical method for free surface flows passing rigidly mounted obstacles» // Computers and Fluids, Vol. 148, (2017), pp. 56-69. PDF
[5] K. Nikitin, K. Terekhov, M. Olshanskii, Y. Vassilevski. «A semi-largangian method on dynamically adapted octree meshes» // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol. 30, No. 6, (2015), pp. 363-380. PDF
[6] K. Nikitin, M. Olshanskii, K. Terekhov, Y. Vassilevski. «A splitting method for numerical simulation of free surface flows of incompressible fluids with surface tension» // Computational Methods in Applied Mathematics, 2014, DOI:10.1515/cmam-2014-0025 PDF
[7] A. Danilov, K. Nikitin, M. Olshanksii, K. Terekhov, Y. Vassilevski. «A unified approach for computing tsunami, waves, floods, and landslides» // Numerical mathematics and advanced applications – ENUMATH 2013 / Lecture Notes in Computational Science and Engineering, Vol. 103, (2015). PDF
[8] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Yu.V.Vassilevski. «CFD technology for 3D simulation of large-scale hydrodynamic events and disasters.» // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol.27, No.4, (2012), pp.399–412. PDF
[9] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Yu.V.Vassilevski. «A numerical method for the simulation of free surface flows of viscoplastic fluid in 3D.» // Journal of Computational Mathematics, Vol.29, No.6, 2011, 605–622. PDF
[10] K.D.Nikitin «Finite volume method for advection-diffusion equation and multiphase flows», Ph.D. thesis, 2010. PDF (in Russian)
[11] K.D.Nikitin. «Realistic free surface flow modelling on adaptive octree meshes.» // SpbGU ITMO, Vol.70, No.6, (2010), pp.60-64. (in Russian)
[12] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Y.V.Vassilevski. «Preserving distance property of level set function and simulation of free surface flows on adaptive grids» // Numerical geometry, grid generation and high perfomance computing, (2010), pp.25-32.
[13] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Yu.V.Vassilevski, "Numerical simulations of free surface flows on adaptive cartesian grids with level set function method" // submitted, November 2010. PDF
[14] K.D.Nikitin, Yu.V.Vassilevski. «Free surface flow modelling on dynamically refined hexahedral meshes.» // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol.23, No.5, (2008), pp.469-485. PDF
[15] K.D.Nikitin. «Computational technology for free surface flows with the use of dynamic hexahedral meshes.» // Computational Methods, Parallel Computing and Information Technology, MSU Publishing House, (2008), pp.183–193. (in Russian)
Nonlinear FV methods for advection-diffusion and multi-phase flows
[16] I.Berre, et al. Verification benchmarks for single-phase flow in three-dimensional fractured porous media. // Advances in Water Resourcesthis, 2021, 147, 103759.
[17] R.Yanbarisov, K.Nikitin. Projection-based monotone embedded discrete fracture method for flow and transport in porous media. // Journal of Computational and Applied Mathematics, 2021, 392, 113484.
[18] K.Nikitin, R.Yanbarisov. Monotone embedded discrete fractures method for flows in porous media. // Journal of Computational and Applied Mathematics, 2020, 365, 112353.
[19] V.Kramarenko, K.Nikitin, Y.Vassilevski. A finite volume scheme with improved well modeling in subsurface flow simulation. // Computational Geosciences, 2017. DOI: 10.1007/s10596-017-9685-5. cg-knv-v3.pdf
[20] И.В.Капырин, К.Д.Никитин, А.В.Расторгуев, В.В.Сускин. Верификация моделей ненасыщенной фильтрации и переноса в зоне аэрации на примере расчетного кода GeRa // Вопросы атомной науки и техники, серия Математическое моделирование физических процессов, No. 1, (2017), С.60-75.
[21] K.Nikitin, K.Novikov, Y.Vassilevski. Nonlinear finite volume method with discrete maximum principle for the two-phase flow model // Lobachevskii Journal of Mathematics, Vol.37, No.5, (2016), 570–581. http://dx.doi.org/10.1134/S1995080216050097
[22] K.Nikitin, V.Kramarenko, Y. Vassilevski. Enhanced Nonlinear Finite Volume Scheme for Multiphase Flows // ECMOR-XV, 2016. http://www.earthdoc.org/publication/publicationdetails/?publication=86236
[23] V.Kramarenko, K.Nikitin, Y.Vassilevski. A nonlinear correction FV scheme for near-well regions. // Finite Volumes for Complex Applications VIII, 2017.
[24] I.Konshin, I.Kapyrin, K.Nikitin, K.Terekhov. Application of the parallel INMOST platform to subsurface flow and transport modelling // Parallel Processing and Applied Mathematics, Lecture Notes in Computer Science, Vol.9574, (2016), 277-286. http://dx.doi.org/10.1007/978-3-319-32152-3_26
[25] K.D.Nikitin, K.M.Terekhov, Y.V.Vassilevski, «Multiphase flows – nonlinear monotone FV scheme and dynamic grids» // ECMOR XIV - 14th European conference on the mathematics of oil recovery, (2014).
[26] I.V.Kapyrin, K.D.Nikitin, K.M.Terekhov, Y.V.Vassilevski, «Nonlinear monotone FV schemes for radionuclide geomigration and multiphase flow models» // Finite Volumes for Complex Applications VII-Elliptic, Parabolic and Hyperbolic Problems. – Springer International Publishing, (2014), pp. 655-663.
[27] K.D.Nikitin, K.M.Terekhov, Y.V.Vassilevski, «A monotone nonlinear finite volume method for diffusion equations and multiphase flows» // Computational Geosciences: Vol. 18, No 3 (2014), pp 311-324, DOI: 10.1007/s10596-013-9387-6. nik-ter-vas-13.pdf
[28] K.D.Nikitin, Y.V.Vassilevski. «A monotone non-linear finite volume method for advection-diffusion equations and multiphase flows.» // 13th European Conference on the Mathematics of Oil Recovery, (2012), pp.1-21. PDF
[29] K.Nikitin, A.Danilov, I.Kapyrin, Yu.Vassilevski. «Application of nonlinear monotone finite volume schemes to advection-diffusion problems.» // Finite Volumes for Complex Applications VI – Problems & Perspectives, Vol.1, (2011), pp.761-769.
[30] K.D.Nikitin, Y.V.Vassilevski. «A monotone finite folume method for advection-diffusion equations on unstructured polyhedral meshes in 3D.» // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol.25, No.4, (2010), pp.335-358. PDF
[31] К.Д.Никитин. «Нелинейный метод конечных объемов для задач двухфазной фильтрации.» // Математическое моделирование, Т.22, №11, (2010), С.131-147 PDF
K.D.Nikitin. «Nonlinear finite volume method for two-phase flows.» // Mathematical Modelling, Vol.22, No.11, (2010), pp.131-147. (in Russian)
The research was supported by
- Russian Science Foundation grants 18-71-10111;
- RFBR grants 12-01-31275, 12-01-33084, 14-01-00830, 15-35-20991 and 17-01-00886;
- Federal program grants № P1127, P753, 02.740.11.0746, 14.740.11.1389 and 14.514.11.4057;
- Russian President grant MK-7159.2013.1 and MK-2951.2017.1.
Visualization
Octree-MAC method
Simulation of the flow around cylinder with circular cross-section in inviscid limit with grid refined towards absolute value of vorticity. Colored in absolute value of vorticity.
Metro Station
Sayano–Shushenskaya Dam
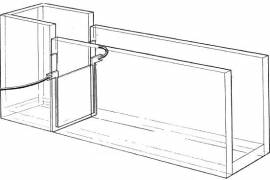
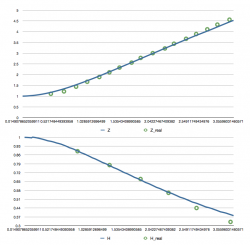
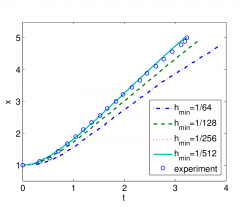
The breaking dam problem
1) The schematic apparatus from J. Martin, W. Moyce, Philos.Trans.R.Soc.Lond.Ser.A, V. 244 (1952), 2) animated numerical solution with the velocity field 3-4) comparison with the experimental data