Table of Contents
Free surface flows research group:
- Yuri Vassilevski (deputy director of INM RAS, professor at MSU, professor at MIPT, head of laboratory in Sechenov University)
- Kirill Nikitin (Ph.D., senior researcher at INM RAS)
- Kirill Terekhov (Ph.D., senior researcher at INM RAS)
- Alexey Chernyshenko (Ph.D., researcher at INM RAS)
- Ruslan Yanbarisov (junior researcher at INM RAS)
Publications
[1] K. Nikitin, Y.Vassilevski, R.Yanbarisov, “An implicit scheme for simulation of free surface non-Newtonian fluid flows on dynamically adapted grids” // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol. 36, I. 3, (June 2021), pp. 165-176. PDF
[2] R.Yanbarisov, Y.Efremov, N.Kosheleva, P.Timashev, Y.Vassilevski, “Numerical Modelling of Multicellular Spheroid Compression: Viscoelastic Fluid vs. Viscoelastic Solid” // Mathematics, Vol. 9, I. 18, (September 2021), DOI:10.3390/math9182333. PDF
[3] K. Nikitin, K.Terekhov, Y.Vassilevski, “Two methods of surface tension treatment in free surface flow simulations” // Applied Mathematics Letters, Vol. 86, (December 2018), pp. 236-242. PDF
[4] K. Nikitin, M.Olshanskii, K.Terekhov, Y.Vassilevski, “A splitting method for free surface flows over partially submerged obstacles” // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol. 33, No. 2, (2018), pp. 95-110. PDF
[5] K. Nikitin, M. Olshanskii, K. Terekhov, Y. Vassilevski, R. Yanbarisov. “An adaptive numerical method for free surface flows passing rigidly mounted obstacles” // Computers and Fluids, Vol. 148, (2017), pp. 56-69. PDF
[6] K. Nikitin, K. Terekhov, M. Olshanskii, Y. Vassilevski. “A semi-largangian method on dynamically adapted octree meshes” // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol. 30, No. 6, (2015), pp. 363-380. PDF
[7] K. Nikitin, M. Olshanskii, K. Terekhov, Y. Vassilevski. “A splitting method for numerical simulation of free surface flows of incompressible fluids with surface tension” // Computational Methods in Applied Mathematics, 2014, DOI:10.1515/cmam-2014-0025 PDF
[8] A. Danilov, K. Nikitin, M. Olshanksii, K. Terekhov, Y. Vassilevski. “A unified approach for computing tsunami, waves, floods, and landslides” // Numerical mathematics and advanced applications – ENUMATH 2013 / Lecture Notes in Computational Science and Engineering, Vol. 103, (2015). PDF
[9] M.A.Olshanskii, K.M.Terekhov, Yu.V.Vassilevski. “An octree-based solver for the incompressible Navier-Stokes equations with enhanced stability and low dissipation” // Computers and Fluids, (2013). PDF
[10] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Yu.V.Vassilevski. “CFD technology for 3D simulation of large-scale hydrodynamic events and disasters.” // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol.27, No.4, (2012), pp.399–412. PDF
[11] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Yu.V.Vassilevski. “A numerical method for the simulation of free surface flows of viscoplastic fluid in 3D.” // Journal of Computational Mathematics, Vol.29, No.6, 2011, 605–622. PDF
[12] K.D.Nikitin “Finite volume method for advection-diffusion equation and multiphase flows”, Ph.D. thesis, 2010. PDF (in Russian)
[13] K.D.Nikitin. “Realistic free surface flow modelling on adaptive octree meshes.” // SpbGU ITMO, Vol.70, No.6, (2010), pp.60-64. (in Russian)
[14] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Y.V.Vassilevski. “Preserving distance property of level set function and simulation of free surface flows on adaptive grids” // Numerical geometry, grid generation and high perfomance computing, (2010), pp.25-32.
[15] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Yu.V.Vassilevski, "Numerical simulations of free surface flows on adaptive cartesian grids with level set function method" // submitted, November 2010. PDF
[16] K.D.Nikitin, Yu.V.Vassilevski. “Free surface flow modelling on dynamically refined hexahedral meshes.” // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol.23, No.5, (2008), pp.469-485. PDF
[17] K.D.Nikitin. “Computational technology for free surface flows with the use of dynamic hexahedral meshes.” // Computational Methods, Parallel Computing and Information Technology, MSU Publishing House, (2008), pp.183–193. (in Russian)
The research is supported by
- RFBR grants 11-01-00971-a, 12-01-00283-a, 12-01-91330-NNIO_a, 12-01-31275-mol_a and 14-01-00830;
- Federal program grants № P753, 02.740.11.0746, 14.740.11.1389 and 14.514.11.4057;
- Russian Science Foundation grant 14-11-00434.
Visualization
Viscoelastic drop fall on solid wall
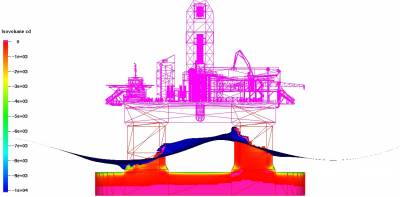
Flow around an oil platform
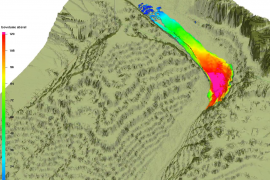
Genaldon glacier disaster
Octree-MAC method
Simulation of the flow around cylinder with circular cross-section in inviscid limit with grid refined towards absolute value of vorticity. Colored in absolute value of vorticity.
Metro Station
Sayano–Shushenskaya Dam
Viscoplastic dam break flow over incline plane
Dam break flow over incline plane with alpha = 18°.
Herschel-Bulkley fluid with K = 47.68 Pa/s^n, n = 0.415, tau_s = 89 Pa.
Freely oscillating viscoplastic droplet
- No plasticity: K = 1/150, tau_s = 0.
- Low plasticity: K = 1/150, tau_s = 0.02.
- High plasticity: K = 1/150, tau_s = 0.04.
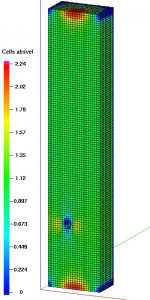
A von Karman vortex street behind cylinder
1) Semi-Lagrangian method (2nd order interpolation), 2) Semi-Lagrangian method (3srd order interpolation), 3) 2nd order upwind TVD
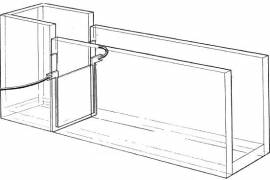
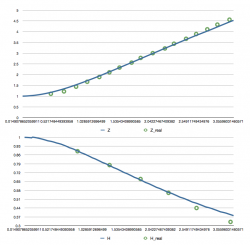
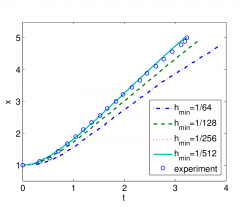
The breaking dam problem
1) The schematic apparatus from J. Martin, W. Moyce, Philos.Trans.R.Soc.Lond.Ser.A, V. 244 (1952), 2) animated numerical solution with the velocity field 3-4) comparison with the experimental data