Research

This is an old revision of the document!

Work group under the head of Yuri Vassilevski:

Yuri Vassilevski (deputy director of INM RAS, professor at MSU)
Kirill Nikitin (Ph.D., researcher at INM RAS)
Maxim Olshanskii (professor at MSU)
Kirill Terekhov (Ph.D. student at INM RAS)
Alexey Chernyshenko (Ph.D. student at INM RAS)

Publications

[1] K.D.Nikitin, Yu.V.Vassilevski. “Free surface flow modelling on dynamically refined hexahedral meshes.” // Russian Journal of Numerical Analysis and Mathematical Modelling, Vol.23, No.5, (2008), pp.469-485.

[2] К.Д.Никитин. “Технология расчёта течений со свободной границей с использованием динамических гексаэдральных сеток.” // Численные методы, параллельные вычисления и информационные технологии: Сборник научных трудов / Под ред. Вл.В.Воеводина и Е.Е.Тыртышникова, Изд-во МГУ, (2008), с.183-198.

[3] К.Д.Никитин, А.Ф.Сулейманов, К.М.Терехов. “Технология моделирования течений со свободной поверхностью в реалистичных сценах.” // Труды математического общества им. Н.И.Лобачевского, Казань: Казан.матем.об-во, T.39, (2009), с.305-307.

[4] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Yu.V.Vassilevski, "Numerical simulations of free surface flows on adaptive cartesian grids with level set function method" // submitted, November 2010. notv9.pdf

[5] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Y.V.Vassilevski. “Preserving distance property of level set function and simulation of free surface flows on adaptive grids” // Численная геометрия, построение расчетных сеток и высокопроизводительные вычисления, (2010), pp.25-32.

[6] К.Д.Никитин. “Реалистичное моделирование свободной водной поверхности на адаптивных сетках типа восьмеричное дерево.” // Научно-технический вестник СПбГУ ИТМО, Т.70, №6, (2010), С.60-64.

[7] К.Д.Никитин “Метод конечных объемов для задачи конвекции-диффузии и моделей двухфазных течений”, Кандидатская диссертация, 2010. nikitin-thesis.pdf

[8] K.D.Nikitin, M.A.Olshanskii, K.M.Terekhov, Y.V.Vassilevski. “A numerical method for the simulation of viscoplastic fluid free surface flows in 3D” // to appear in J.Comp.Math. fsvisc2011.pdf

The research is supported by

RFBR grants 08-01-00159-а, 09-01-00115-а and 11-01-00971-a;
Federal program grants № П1127, П753 and 02.740.11.0746.

Visualizations:

Metro Station (2011)

Flooding of the Polezhaevskaya Moscow Metro Station

Sayano–Shushenskaya Dam (2011)

1) Break of the Sayano–Shushenskaya Dam, 2) Landslide over the Sayano–Shushenskaya Dam

Viscoplastic dam break flow over incline plane. (2011, [1])

Dam break flow over incline plane with alpha = 18°.
Herschel-Bulkley fluid with K = 47.68 Pa/s^n, n = 0.415, tau_s = 89 Pa.

Freely oscillating viscoplastic droplet (2011, [1])

No plasticity: K = 1/150, tau_s = 0.
Low plasticity: K = 1/150, tau_s = 0.02.
High plasticity: K = 1/150, tau_s = 0.04.

A von Karman vortex street behind cylinder. (2011)

1) Semi-Lagrangian method (2nd order interpolation), 2) Semi-Lagrangian method (3srd order interpolation), 3) 2nd order upwind TVD

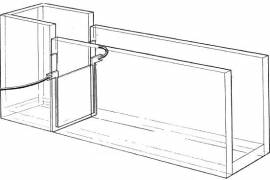
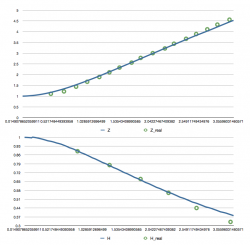
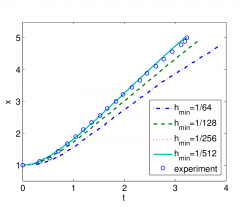
The breaking dam problem

1) The schematic apparatus from J. Martin, W. Moyce, Philos.Trans.R.Soc.Lond.Ser.A, V. 244 (1952), 2) animated numerical solution with the velocity field 3-4) comparison with the experimental data